|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 |
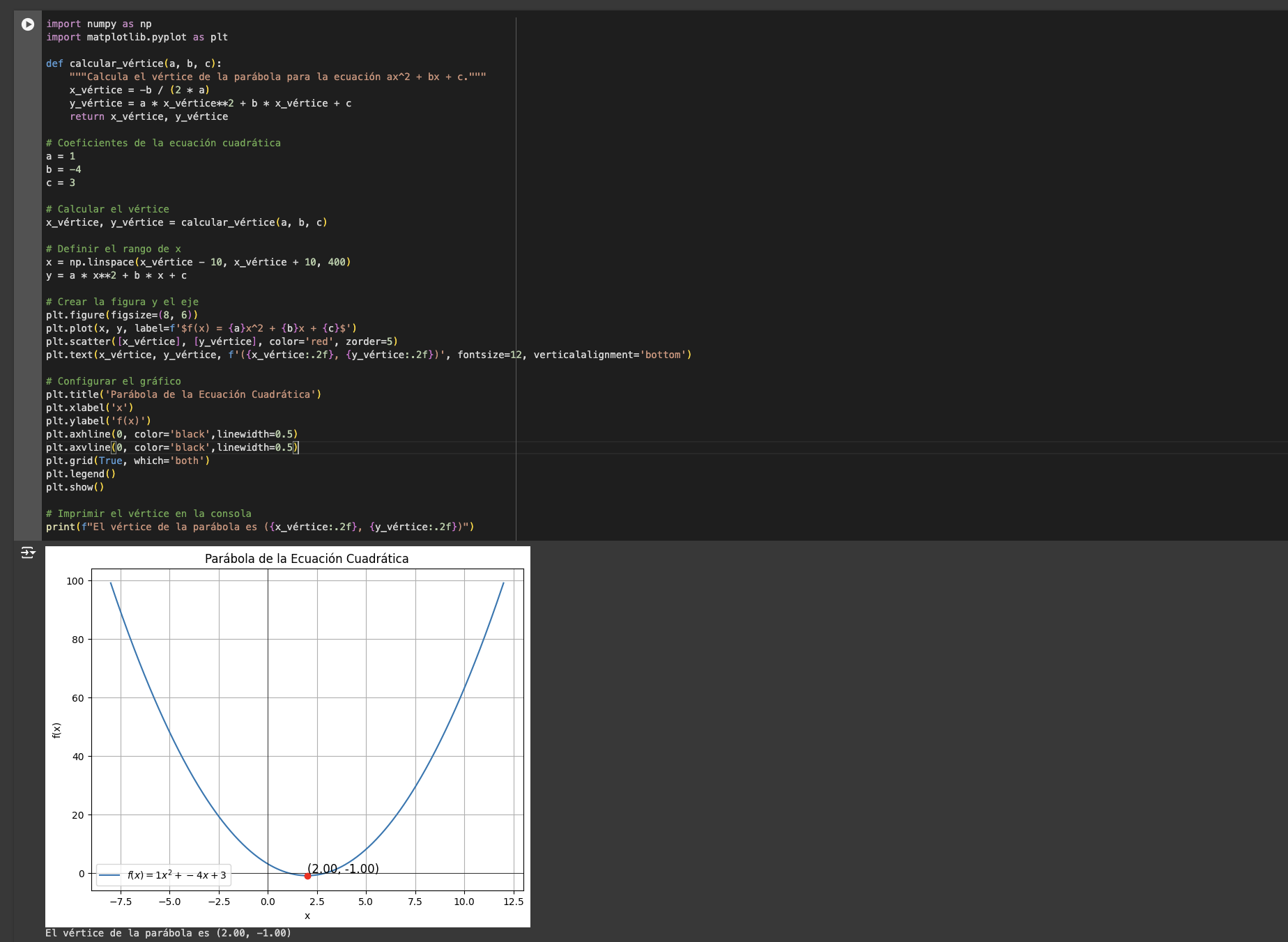
import numpy as np import matplotlib.pyplot as plt def calcular_vértice(a, b, c): """Calcula el vértice de la parábola para la ecuación ax^2 + bx + c.""" x_vértice = -b / (2 * a) y_vértice = a * x_vértice**2 + b * x_vértice + c return x_vértice, y_vértice # Coeficientes de la ecuación cuadrática a = 1 b = -4 c = 3 # Calcular el vértice x_vértice, y_vértice = calcular_vértice(a, b, c) # Definir el rango de x x = np.linspace(x_vértice - 10, x_vértice + 10, 400) y = a * x**2 + b * x + c # Crear la figura y el eje plt.figure(figsize=(8, 6)) plt.plot(x, y, label=f'$f(x) = {a}x^2 + {b}x + {c}$') plt.scatter([x_vértice], [y_vértice], color='red', zorder=5) plt.text(x_vértice, y_vértice, f'({x_vértice:.2f}, {y_vértice:.2f})', fontsize=12, verticalalignment='bottom') # Configurar el gráfico plt.title('Parábola de la Ecuación Cuadrática') plt.xlabel('x') plt.ylabel('f(x)') plt.axhline(0, color='black',linewidth=0.5) plt.axvline(0, color='black',linewidth=0.5) plt.grid(True, which='both') plt.legend() plt.show() # Imprimir el vértice en la consola print(f"El vértice de la parábola es ({x_vértice:.2f}, {y_vértice:.2f})") |
Explicación del código
- Función
calcular_vértice:- Calcula las coordenadas xxx y yyy del vértice de la parábola para una ecuación cuadrática dada por los coeficientes aaa, bbb y ccc.
- Definición de Coeficientes:
- Asigna valores a aaa, bbb y ccc. Puedes cambiar estos valores para probar diferentes ecuaciones cuadráticas.
- Generación de Datos:
- Usa
numpypara crear un rango de valores de xxx y calcular los valores correspondientes de yyy.
- Usa
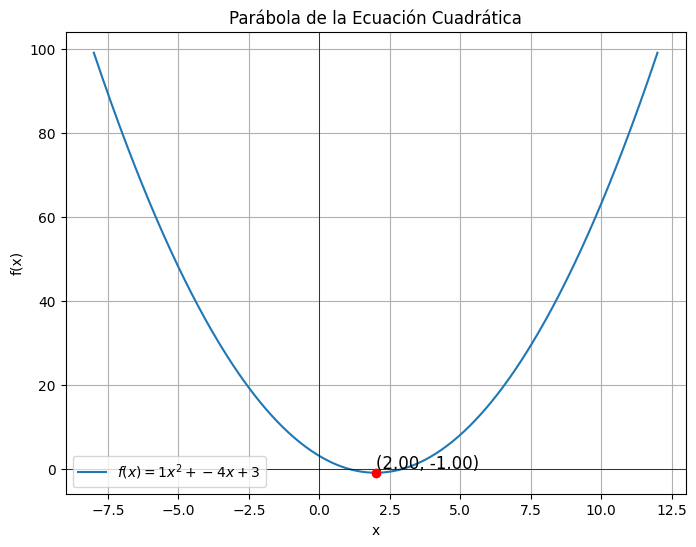
- Creación del Gráfico:
- Utiliza
matplotlibpara graficar la parábola y marcar el vértice con un punto rojo. También muestra las coordenadas del vértice en el gráfico.
- Utiliza
- Impresión en Consola:
- Imprime las coordenadas del vértice en la consola.